AtCoder Beginner Contest 264のA~E問題を解いたので、その解説や感想などを書いていきます!
緑コーダーなので、それ以上の方には役立たない内容だと思います。
同じ緑コーダーの人や茶、灰コーダーの人の参考になれば幸いです。
言語はPythonです!

A: “atcoder”.substr()
‘atcoder’という文字列から指定された部分を抜き出す問題です。
問題文のタイトルにもある通り、substrみたいな部分的な文字列を抜き出す関数を使うといいかなと思います。
pythonの場合は文字列に対してスライス操作([1:4]みたいなやつ)ができるのでそれで書けば楽ですね。
インデックスが0から始まる点、スライスの最後は含まれない点を考慮する必要があるのは注意です。
コードはこんな感じになりました。
l,r=map(int,input().split()) s = 'atcoder' print(s[l-1:r])
B: Nice Grid
与えられたマス目の指定された点が黒か白かを判定する問題です。
15×15のマス目なのでコード上に力技で書いてしまって、結果を返すのが早い気がします。
こんな感じで書いちゃいました。
r,c=map(int,input().split())
m = [[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],
[0,1,1,1,1,1,1,1,1,1,1,1,1,1,0],
[0,1,0,0,0,0,0,0,0,0,0,0,0,1,0],
[0,1,0,1,1,1,1,1,1,1,1,1,0,1,0],
[0,1,0,1,0,0,0,0,0,0,0,1,0,1,0],
[0,1,0,1,0,1,1,1,1,1,0,1,0,1,0],
[0,1,0,1,0,1,0,0,0,1,0,1,0,1,0],
[0,1,0,1,0,1,0,1,0,1,0,1,0,1,0],
[0,1,0,1,0,1,0,0,0,1,0,1,0,1,0],
[0,1,0,1,0,1,1,1,1,1,0,1,0,1,0],
[0,1,0,1,0,0,0,0,0,0,0,1,0,1,0],
[0,1,0,1,1,1,1,1,1,1,1,1,0,1,0],
[0,1,0,0,0,0,0,0,0,0,0,0,0,1,0],
[0,1,1,1,1,1,1,1,1,1,1,1,1,1,0],
[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]]
print('black' if m[r-1][c-1] == 0 else 'white')
解説を見ると対称性を使うのがよさそうでしたね。
対称性も一瞬頭をよぎりましたが、サイズが15と小さいですし、変なことやって時間を取られるよりは力技の方がいいかなと思ってしまいました。
チェビシェフ距離なるものがあるというのは初めて知ったので、知っておくと次回以降使えるかもですね!
C: Matrix Reducing
大きな行列Aから任意の行、列を取り除くいたら行列Bと一致できるかという問題です。
パッと見て思ったのは、行・列の制約がともに10以下ということなので全通りの組み合わせを試してもいけそうだなということです。
なので、行列Aから残す行・列を全探索して行列A’を作成→行列Bと一致するかをチェックというのを繰り返せばOKです。
行列A’を作成するときは、下の図のように全探索で選ばれた行・列の交わるところを抜き出すようにしました。
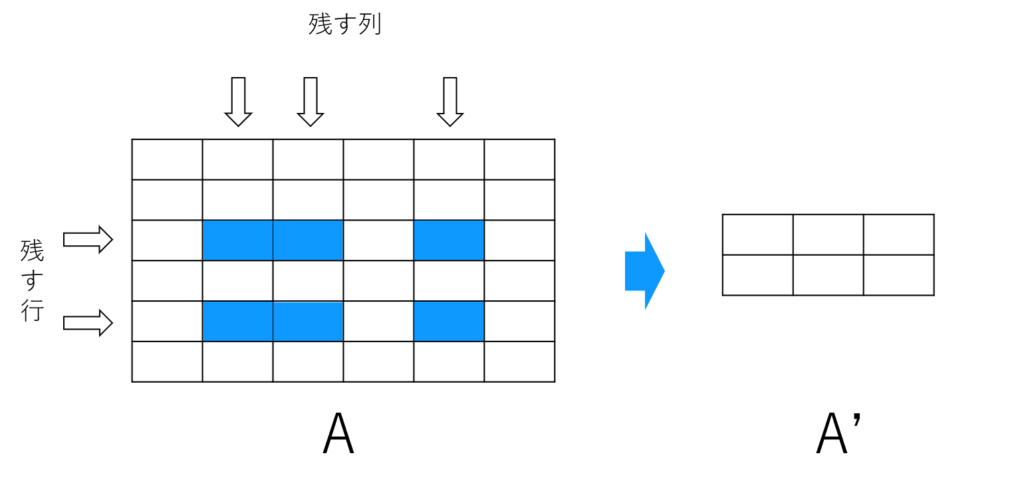
行・列の全探索はPythonのitertools.combinationsを使えば簡単に列挙することができます。
コードはこんな感じです。
import itertools
h1,w1 = map(int,input().split())
A1 = []
for _ in range(h1):
a = list(map(int, input().split()))
A1.append(a)
h2,w2 = map(int,input().split())
A2 = []
for _ in range(h2):
a = list(map(int, input().split()))
A2.append(a)
ok = False
# 使用する行・列を全探索
for h_r in itertools.combinations([i for i in range(h1)], h2):
for w_r in itertools.combinations([j for j in range(w1)], w2):
# 全探索した結果から新しい行列を作る
A1_try = []
for h in h_r:
ro=[]
for w in w_r:
ro.append(A1[h][w])
A1_try.append(ro)
# 判定:全部Bと一致していればループから抜ける
check = True
for i in range(h2):
for j in range(w2):
if not A1_try[i][j] == A2[i][j]:
check = False
break
if check:
ok = True
break
print('Yes' if ok else 'No')
ちなみにコンテスト中は、行列から行・列を取り除く方法が思いつかずに(正確にはnumpy.deleteをつかったけどTLEした)解けなかったんですが、翌日に行・列を取り除くのではなく新しく行列作ればいーじゃんと思いついて解くことができました。
この辺がコンテスト中にひらめけるようになりたいものです。
D: “redocta”.swap(i,i+1)
文字列Sの隣あっている文字列を入れ替えて’atcoder’にするのに必要な最小回数を求める問題です。
文字列に被りもないですし、一番左をaにする→その右隣をtにする→その右隣りをcにする→…と答えが’atcoder’になるまで文字を入れ替えればできるのではと思いました。
それを愚直に実装したら無事正解できました!
s = input()
def check(ss):
if ss == 'atcoder':
return True
else:
return False
ans = 0
while True:
if check(s):
break
s1 = list(s)
if s1[0] != 'a':
pos = s.find('a')
s1[pos] = s1[pos-1]
s1[pos-1] = 'a'
elif s1[1] != 't':
pos = s.find('t')
s1[pos] = s1[pos-1]
s1[pos-1] = 't'
elif s1[2] != 'c':
pos = s.find('c')
s1[pos] = s1[pos-1]
s1[pos-1] = 'c'
elif s1[3] != 'o':
pos = s.find('o')
s1[pos] = s1[pos-1]
s1[pos-1] = 'o'
elif s1[4] != 'd':
pos = s.find('d')
s1[pos] = s1[pos-1]
s1[pos-1] = 'd'
elif s1[5] != 'e':
pos = s.find('e')
s1[pos] = s1[pos-1]
s1[pos-1] = 'e'
elif s1[6] != 'r':
pos = s.find('r')
s1[pos] = s1[pos-1]
s1[pos-1] = 'r'
s = ''.join(s1)
ans += 1
print(ans)
見れば見るほど、力技ですね…
今回は7文字&ゴールが’atcoder’固定という制限があったので何とかなりましたが、文字数が多い場合はおそらく不可能ですね。
解説を読むと転倒数なるものがあるらしいので、こちらも調べておきたいです。
E: Blackout 2
複数の都市と複数の発電所が電線でつながれている状態から、どんどん電線が切断されていきます。
電線が切断されたときに、発電所につながっている都市の数を求める問題です。
こういう問題みたいに、いくつかのものをどんどん合体させてひとつのグループにさせるときはUnion-Findを使うとよいですね!
(Union-Findの詳細はこちらの記事が詳しいです!実装もここからパクっています。)
ただ、Union-Findはどんどん合体させるのは得意でも、分割することはできないという弱点があるのでそのまま適用するわけにはいかないです。
なので、「電線がどんどん切断される」というQ個のイベントを逆に考えます。
すると、初めにいくつかの都市と発電所が接続されている状態から、どんどんグループ同士を合体させるという問題へと言い換えることができます。
これならUnion-Findを使って考えることができます!
また、グループに発電所が入っているか?を判定する必要がありますが、毎回検索していては時間が足りないので、別途フラグ配列を用意してUnion-Findの根要素のインデックスを見れば発電所に接続されているかを判定できるようにします。
というわけでこんな感じのコードかいたら動きました。
from collections import defaultdict, Counter
# この実装はhttps://note.nkmk.me/python-union-find/からもってきた
class UnionFind():
def __init__(self, n):
self.n = n
self.parents = [-1] * n
def find(self, x):
if self.parents[x] < 0:
return x
else:
self.parents[x] = self.find(self.parents[x])
return self.parents[x]
def union(self, x, y):
x = self.find(x)
y = self.find(y)
if x == y:
return
if self.parents[x] > self.parents[y]:
x, y = y, x
self.parents[x] += self.parents[y]
self.parents[y] = x
# 根要素のインデックスをとれるように魔改造
def get_root(self, x):
tmp = self.find(x)
return tmp if tmp >= 0 else x
def size(self, x):
return -self.parents[self.find(x)]
def same(self, x, y):
return self.find(x) == self.find(y)
def members(self, x):
root = self.find(x)
return [i for i in range(self.n) if self.find(i) == root]
def roots(self):
return [i for i, x in enumerate(self.parents) if x < 0]
def group_count(self):
return len(self.roots())
def all_group_members(self):
group_members = defaultdict(list)
for member in range(self.n):
group_members[self.find(member)].append(member)
return group_members
def __str__(self):
return '\n'.join(f'{r}: {m}' for r, m in self.all_group_members().items())
n,m,e = map(int,input().split())
# 接続する組をいったん保存しておく
uvlist = []
for i in range(e):
u,v = map(int,input().split())
uvlist.append((u-1,v-1))
# イベントを保存
q = int(input())
X = []
for _ in range(q):
x = int(input())
X.append(x-1)
# 素早く検索できるように辞書に入れる
Xdict = Counter(X)
# 各地点が発電所につながっているかのフラグ配列
# Union-Findの根要素のインデックスを見れば接続されているかわかる
hasPower = [0]*(n+m)
for i in range(m):
hasPower[i+n] = 1
ans = [0]*(q+1)
uf = UnionFind(n+m)
# まずはイベントで切断されるところ以外を合体させる
for idx, uv in enumerate(uvlist):
# イベントで切断(接続?)するので無視
if idx in Xdict:
continue
# 片方だけ発電所に接続されているならフラグ更新&接続される都市をカウント
if hasPower[uf.get_root(uv[0])] == 1 and hasPower[uf.get_root(uv[1])] == 0:
ans[0] += uf.size(uv[1])
hasPower[uf.get_root(uv[1])] = 1
elif hasPower[uf.get_root(uv[0])] == 0 and hasPower[uf.get_root(uv[1])] == 1:
ans[0] += uf.size(uv[0])
hasPower[uf.get_root(uv[0])] = 1
uf.union(uv[0],uv[1])
# イベントを逆に回しながら接続していく
for idx, i in enumerate(reversed(X)):
uv = uvlist[i]
ans[idx+1] = ans[idx]
if hasPower[uf.get_root(uv[0])] == 1 and hasPower[uf.get_root(uv[1])] == 0:
ans[idx+1] += uf.size(uv[1])
hasPower[uf.get_root(uv[1])] = 1
elif hasPower[uf.get_root(uv[0])] == 0 and hasPower[uf.get_root(uv[1])] == 1:
ans[idx+1] += uf.size(uv[0])
hasPower[uf.get_root(uv[0])] = 1
uf.union(uv[0],uv[1])
# イベントを逆にしたので、出力する答えは逆順
for a in reversed(ans[:-1]):
print(a)
コンテスト中はUnion-Find使う?とか思っていましたが、切断するのができなくてあきらめてしまいました。
イベントを逆にたどればよかったんですね!
いやー、こういうのはどうやったら思いつくようになるんでしょうか…
まとめ
今回はA, B, D問題に正解という結果になってしまいました。
C問題もおしいところまではいけていましたが、途中でめんどくさくなったのがいけませんね…
行・列を取り除くのが難しい→あらたに行列をつくればよいという発想の切り替えができるようになりたいものです。
E問題もとっかかりを少しだけ思いつきはしましたが、コンテスト中に解ききるには実装面・ひらめき面でまだ精進が必要です…
あとはチェビシェフ距離や転倒数とかを調べておきたいですね。
おしまい。



コメント